
We show that the use of midpoint LHS as the initial design increases the efficiency and robustness of the resulting MCSs and NIPCE meta-models.
The analysis is based on two case studies involving numerical simulation of density dependent flow and solute transport in porous media within the context of seawater intrusion in coastal aquifers.
Latin hypercube sampling rmp full#
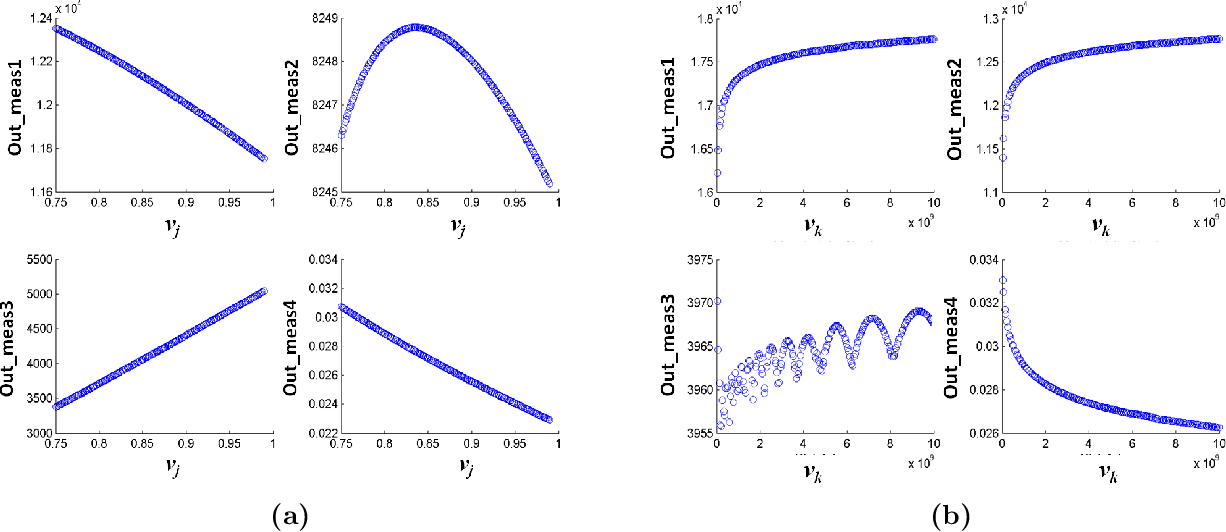
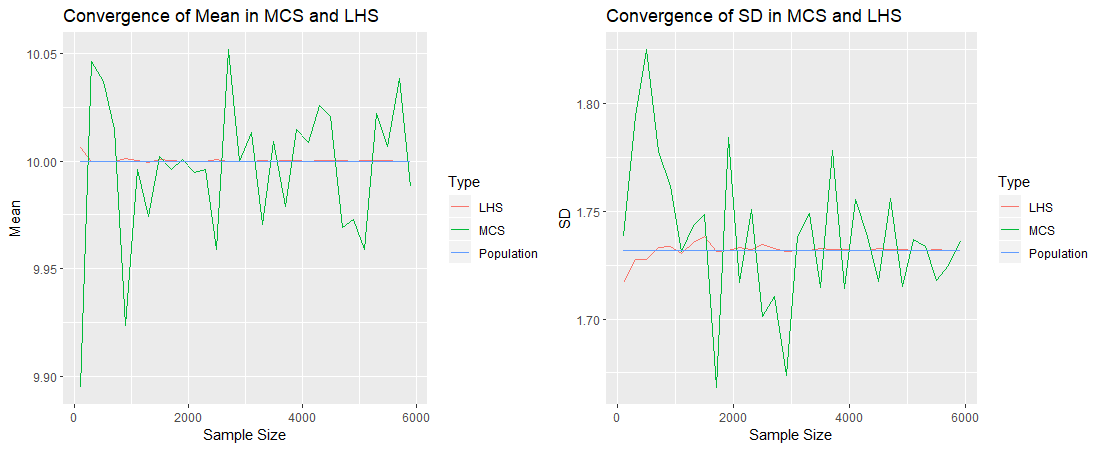
The two approaches are compared by incorporating their resulting sample designs in Monte Carlo simulation (MCS) for uncertainty propagation analysis, and then, by employing the sample designs in the selection of the training set for constructing non-intrusive polynomial chaos expansion (NIPCE) meta-models which subsequently replace the original full model in MCSs. It is also illustrated that the space-filling characteristics of OLHS designs based on midpoint LHS are significantly better those based on random LHS. In this study we compare the two approaches and show that the space-filling characteristics of OLHS designs are sensitive to the initial design that is fed into the optimization algorithm. Both approaches have been extensively used, but no attempt has been previously made to compare the efficiency and robustness of their resulting sample designs. Previous studies, as well as codes developed for OLHS, have relied on one of the following two approaches for the selection of the initial design in OLHS: (1) the use of random points in the hypercube intervals (random LHS), and (2) the use of midpoints in the hypercube intervals (midpoint LHS). However, little attention has been given to the impact of the initial design that is fed into the optimization algorithm, on the efficiency of OLHS strategies. The majority of literature regarding optimized Latin hypercube sampling (OLHS) is devoted to increasing the efficiency of these sampling strategies through the development of new algorithms based on the combination of innovative space-filling criteria and specialized optimization schemes.


 0 kommentar(er)
0 kommentar(er)
